Some butterflies have shiny, vividly colored wings. From different angles you see different colors. This effect is called iridescence. How does it work?
It turns out these butterfly wings are made of very fancy materials! Light bounces around inside these materials in a tricky way. Sunlight of different colors winds up reflecting off these materials in different directions.
We’re starting to understand the materials and make similar substances in the lab. They’re called photonic crystals. They have amazing properties.
Here at the Centre for Quantum Technologies we have people studying exotic materials of many kinds. Next door, there’s a lab completely devoted to studying graphene: crystal sheets of carbon in which electrons can move as if they were massless particles! Graphene has a lot of potential for building new technologies—that’s why Singapore is pumping money into researching it.
Some physicists at MIT just showed that one of the materials in butterfly wings might act like a 3d form of graphene. In graphene, electrons can only move easily in 2 directions. In this new material, electrons could move in all 3 directions, acting as if they had no mass.
The pictures here show the microscopic structure of two materials found in butterfly wings:
The picture at left actually shows a sculpture made by the mathematical artist Bathsheba Grossman. But it’s a piece of a gyroid: a surface with a very complicated shape, which repeats forever in 3 directions. It’s called a minimal surface because you can’t shrink its area by tweaking it just a little. It divides space into two regions.
The gyroid was discovered in 1970 by a mathematician, Alan Schoen. It’s a triply periodic minimal surfaces, meaning one that repeats itself in 3 different directions in space, like a crystal.
Schoen was working for NASA, and his idea was to use the gyroid for building ultra-light, super-strong structures. But that didn’t happen. Research doesn’t move in predictable directions.
In 1983, people discovered that in some mixtures of oil and water, the oil naturally forms a gyroid. The sheets of oil try to minimize their area, so it’s not surprising that they form a minimal surface. Something else makes this surface be a gyroid—I’m not sure what.
Butterfly wings are made of a hard material called chitin. Around 2008, people discovered that the chitin in some iridescent butterfly wings is made in a gyroid pattern! The spacing in this pattern is very small, about one wavelength of visible light. This makes light move through this material in a complicated way, which depends on the light’s color and the direction it’s moving.
So: butterflies have naturally evolved a photonic crystal based on a gyroid!
The universe is awesome, but it’s not magic. A mathematical pattern is beautiful if it’s a simple solution to at least one simple problem. This is why beautiful patterns naturally bring themselves into existence: they’re the simplest ways for certain things to happen. Darwinian evolution helps out: it scans through trillions of possibilities and finds solutions to problems. So, we should expect life to be packed with mathematically beautiful patterns… and it is.
The picture at right above shows a ‘double gyroid’. Here it is again:
This is actually two interlocking surfaces, shown in red and blue. You can get them by writing the gyroid as a level surface:
and taking the two nearby surfaces
for some small value of 
It turns out that while they’re still growing, some butterflies have a double gyroid pattern in their wings. This turns into a single gyroid when they grow up!
The new research at MIT studied how an electron would move through a double gyroid pattern. They calculated its dispersion relation: how the speed of the electron would depend on its energy and the direction it’s moving.
An ordinary particle moves faster if it has more energy. But a massless particle, like a photon, moves at the same speed no matter what energy it has. The MIT team showed that an electron in a double gyroid pattern moves at a speed that doesn’t depend much on its energy. So, in some ways this electron acts like a massless particle.
But it’s quite different than a photon. It’s actually more like a neutrino! You see, unlike photons, electrons and neutrinos are spin-1/2 particles. Neutrinos are almost massless. A massless spin-1/2 particle can have a built-in handedness, spinning in only one direction around its axis of motion. Such a particle is called a Weyl spinor. The MIT team showed that a electron moving through a double gyroid acts approximately like a Weyl spinor!
How does this work? Well, the key fact is that the double gyroid has a built-in handedness, or chirality. It comes in a left-handed and right-handed form. You can see the handedness quite clearly in Grossman’s sculpture of the ordinary gyroid:
Beware: nobody has actually made electrons act like Weyl spinors in the lab yet. The MIT team just found a way that should work. Someday someone will actually make it happen, probably in less than a decade. And later, someone will do amazing things with this ability. I don’t know what. Maybe the butterflies know!
References and more
For a good introduction to the physics of gyroids, see:
• James A. Dolan, Bodo D. Wilts, Silvia Vignolini, Jeremy J. Baumberg, Ullrich Steiner and Timothy D. Wilkinson, Optical properties of gyroid structured materials: from photonic crystals to metamaterials, Advanced Optical Materials 3 (2015), 12–32.
For some of the history and math of gyroids, see Alan Schoen’s webpage:
• Alan Schoen, Triply-periodic minimal surfaces.
For more on gyroids in butterfly wings, see:
• K. Michielsen and D. G. Stavenga, Gyroid cuticular structures in butterfly wing scales: biological photonic crystals.
• Vinodkumar Saranathana et al, Structure, function, and self-assembly of single network gyroid (I4132) photonic crystals in butterfly wing scales, PNAS 107 (2010), 11676–11681.
The paper by Michielsen and Stavenga is free online! They say the famous ‘blue Morpho’ butterfly shown in the picture at the top of this article does not use a gyroid; it uses a “two-dimensional photonic crystal slab consisting of arrays of rectangles formed by lamellae and microribs.” But they find gyroids in four other species: Callophrys rubi, Cyanophrys remus, Pardes sesostris and Teinopalpus imperialis. It compares tunnelling electron microscope pictures of slices of their iridescent patches with computer-generated slices of gyroids. The comparison looks pretty good to me:
For the evolution of iridescence, see:
• Melissa G. Meadows et al, Iridescence: views from many angles, J. Roy. Soc. Interface 6 (2009).
For the new research at MIT, see:
• Ling Lu, Liang Fu, John D. Joannopoulos and Marin Soljačić, Weyl points and line nodes in gapless gyroid photonic crystals.
• Ling Lu, Zhiyu Wang, Dexin Ye, Lixin Ran, Liang Fu, John D. Joannopoulos and Marin Soljačić, Experimental observation of Weyl points, Science 349 (2015), 622–624.
Again, the first is free online. There’s a lot of great math lurking inside, most of which is too mind-blowing too explain quickly. Let me just paraphrase the start of the paper, so at least experts can get the idea:
Two-dimensional (2d) electrons and photons at the energies and frequencies of Dirac points exhibit extraordinary features. As the best example, almost all the remarkable properties of graphene are tied to the massless Dirac fermions at its Fermi level. Topologically, Dirac cones are not only the critical points for 2d phase transitions but also the unique surface manifestation of a topologically gapped 3d bulk. In a similar way, it is expected that if a material could be found that exhibits a 3d linear dispersion relation, it would also display a wide range of interesting physics phenomena. The associated 3D linear point degeneracies are called “Weyl points”. In the past year, there have been a few studies of Weyl fermions in electronics. The associated Fermi-arc surface states, quantum Hall effect, novel transport properties and a realization of the Adler–Bell–Jackiw anomaly are also expected. However, no observation of Weyl points has been reported. Here, we present a theoretical discovery and detailed numerical investigation of frequency-isolated Weyl points in perturbed double-gyroid photonic crystals along with their complete phase diagrams and their topologically protected surface states.
Also a bit for the mathematicians:
Weyl points are topologically stable objects in the 3d Brillouin zone: they act as monopoles of Berry flux in momentum space, and hence are intimately related to the topological invariant known as the Chern number. The Chern number can be defined for a single bulk band or a set of bands, where the Chern numbers of the individual bands are summed, on any closed 2d surface in the 3d Brillouin zone. The difference of the Chern numbers defined on two surfaces, of all bands below the Weyl point frequencies, equals the sum of the chiralities of the Weyl points enclosed in between the two surfaces.
This is a mix of topology and physics jargon that may be hard for pure mathematicians to understand, but I’ll be glad to translate if there’s interest.
For starters, a ‘monopole of Berry flux in momentum space’ is a poetic way of talking about a twisted complex line bundle over the space of allowed energy-momenta of the electron in the double gyroid. We get a twist at every ‘Weyl point’, meaning a point where the dispersion relations look locally like those of a Weyl spinor when its energy-momentum is near zero. Near such a point, the dispersion relations are a Fourier-transformed version of the Weyl equation.
Azimuth 
Neat! So ia a Dirac cone a Dirac string that has gone off its diet, or maybe bulked up on steroids?
I think a Dirac cone is just the cone of allowed energy-momenta for a massless particle:
in units with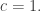
Or, more interestingly, an approximate copy of this cone somewhere in energy-momentum space! If you plot the allowed energy-momenta 
for graphene, which is a 2-dimensional crystal, you get a picture with lots of Dirac cones:
For a gyroid you get something even more complicated (in one dimension higher). This is how we can simulate massless spin-1/2 particles in the lab!
Very pretty! But since the Dirac equation describes massive particles, I don’t understand why these are Dirac cones.
Of course the Dirac equation also describes massless particles: just set the mass to zero. But I agree that this explanation for the name ‘Dirac cone’ sounds dumb—so dumb that it’s hard to believe I’m understanding it correctly.
And yet, a number of sources assure me that a conical singularity in the dispersion relations for a nonchiral spin-1/2 particle is called a Dirac cone, with the tip of a Dirac cone being called a Dirac point. For example, Wikipedia discusses the 6 Dirac points for graphene shown in my picture above:
The mathematically interesting thing is that while graphene gives Dirac points in a 2+1-dimensional field theory, the double gyroid gives Weyl points in a 3+1-dimensional field theory.
The Weyl equation describes a massless chiral spin-1/2 particle in 3+1-dimensional spacetime:
where
are Pauli matrices and 
is a 2-component spinor function on 3+1-dimensonal Minkowski spacetime. Taking the Fourier transform we get
where
is the energy-momentum 4-vector. Some standard fiddling shows that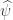 
needs to live on the lightcone in energy-momentum space. So, we’ve got a 
valued function 
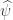on this cone… but the equation
restricts the values this function can take at each point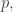
forcing it to live in a 1-dimensional subspace… except at the origin 
The origin is called a ‘Weyl point’.
So, we have a 1-dimensional complex vector bundle on the lightcone minus this Weyl point, and the cool part is that this bundle is nontrivial! It has a ‘twist’ at the Weyl point.
The lightcone with its tip removed is topologically a 2-sphere times a line, and the line is contractible, so we’re really getting a nontrivial complex line bundle on the 2-sphere. There’s one such bundle for each integer—the ‘Chern number’, which counts the twistiness of the bundle. The bundle we’re getting is the one numbered either +1 or -1, depending on whether our spin-1/2 particle is left-handed or right-handed!
(I wrote down one version of the Weyl equation, but there’s another, where we do something like take the complex conjugates of the Pauli matrices, which describes particles of the other handedness.)
If you look in different directions your eyes gaze along different rays in the lightcone, and the possible ways of gazing form a sphere, the ‘heavenly sphere’, which can be seen as the Riemann sphere. You can also see points in this sphere as different possible directions that the energy-momentum of a massless particle can point. They Weyl equation picks out nontrivial complex line bundle on this sphere!
One thing this implies is that as we continuously change the parameters describing a condensed matter system, Weyl points can’t appear or disappear on their: they can only appear or disappear in cancelling pairs. So if I have a condensed matter system that has some sort of left-handed massless spin-1/2 quasiparticle, and I start heating it up or something, that can’t make this type of particle no longer possible. It might, however, make a new type of left-handed quasiparticle possible, along with a corresponding new type of right-handed quasiparticle.
0) That gyroid has some subtle regularities. Did anyone notice that amid the confusion, at the points of joining, the surface normals are all parallel?
1) OK that was kind of a joke. Now a serious if naive question: If the vertical axis in this beautiful plot is E, and massless particles move with the same speed independent of energy, why don’t all of the allowed points lie on the surface of a vertical cylinder centered on the origin?
I didn’t get that joke, arch1. But about this:
I’m not sure I get what you mean, but this sure isn’t a graph of energy as a function of speed! It’s a graph of energy as a function of momentum.
Oh, maybe you’re thinking momentum is proportional to speed? No, that’s only true in certain very special situations, not for massless particles. Photons of violet light have more momentum than photons of red light, but the same speed.
This graph shows energy
as a function of momentum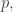 
which is a vector with 2 components in the case of graphene). For a massless particle we have
where
is some constant. This constant is the speed of the particle, which is the usual speed of light when our particle is the photon in the vacuum. So, when the graph of 
as a function of 
looks like a cone, you know you’re dealing with something that acts like a massless particle.
Maybe you’re wondering how we can look at the relation between energy and momentum and figure out the speed of a particle. In quantum mechanics particles are waves, so there are a few different ways to define their speed. The phase velocity (really ‘phase speed’) of a wave is
and the group velocity (really group speed) is
For either kind of speed, if you have
the speed works out to be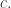
If you want to understand these formulas, click the links!
John, I was indeed assuming that momentum is proportional to speed. I’ll read your remedial instruction (thanks) and follow up on the links.
Re: my joke, I get that a lot. (I’m beginning to think my wife is right about my sense of humor:-) In this case, the intended humor is that the thing I labeled a “subtle regularity” is (I think) just a consequence of how the .GIF was built.
I assume the .GIF shows the gyroid being built up layer by layer, as if the gyroid were being printed by a 3D printer. In which case I think that the surface normal at the points of joining (the points at which two separate pieces of geoid first touch) must be perpendicular to the planes defining the layers that are being added.
Arch1 wrote:
Okay. Yeah, when you first start learning physics, ‘momentum’ seems like a fancy name for mass times velocity, perhaps invented by lazy physicists who prefer to write one letter instead of two.
And once upon a time, maybe people thought that’s all momentum was. But it took on a life of its own and now we realize it’s quite different. If you have a charged particle in a magnetic field, its momentum is not its mass times its velocity. And if you have an ordinary particle and take special relativity into account, its momentum is not just its rest mass times its velocity.
So what is momentum? The real definition of momentum is perhaps easier for waves than for particles. If you have a wave like
where
is time and 
is the position vector, then its energy is 
and its momentum is the vector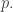 
So, energy says how rapidly a wave oscillates as you move forwards in time, while momentum in any spatial direction says how fast the wave oscillates as you move in that spatial direction.
That’s all there is to it, nowadays.
“If you have a charged particle in an electric field, its momentum is not its mass times its velocity. ….”
Can you elaborate on that (in the simple classical case)? It doesn’t sound like any classical mechanics I know….
Bruce wrote:
Thanks, you caught a mistake. I should have said:
and I’m actually going to go back and change that word in my earlier comment.
First, note something more familiar. The energy of a charged particle in a electric field is not just
there’s a correction due to the scalar potential:
where
is its charge and 
is the scalar potential at the particle’s location. The scalar potential, also known as the electrostatic potential, is the field with
where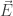
is the electric field.
It turns out that in a similar way, the momentum of a charged particle in a magnetic field is not just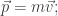
there’s a correction due to the vector potential:
where
is the speed of light and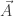 
is the vector potential. The vector potential is the field with
where
is the magnetic field.
All this is nicely explained here.
[…] mathematics, physics, quantum technologies. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own […]
Over on G+, Steve Esterly wrote:
Unfortunately none of the other butterfly pictures I saw were as charismatic as the blue Morpho! But thanks, I edited my post to explain what sort of photonic crystal the Morpho has.
And while we’re on corrections, Alan Schoen pointed out that the double gyroid does not consist of two minimal surfaces; it’s just two surfaces that show up naturally when you write the gyroid as
and take the surfaces
for some small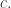
[…] The Physics of Butterfly Wings. […]
I am thinking that the gyroid structure in the butterfly wind is a genetic optimization to obtain stiffness, so that a little deformation give a minimum change in the minimum surface; so that same structure can be possible in other flying insects; It is interesting because a genetic optimization means saving energy, and saving material.
I am thinking that the minimal surface can be classified using the graph that is inner the level surface, that must have periodic structure (a three-dimensional periodic graph) that can have a classification similar to crystallography; so that a deformation of the structure, with the same periodic graph, can have similar properties.
[…] The Physics of Butterfly Wings | Azimuthhttps://johncarlosbaez.wordpress.com/2015/08/11/the-physics-of-butterfly-wings/ […]
A while back I told you about a minimal surface called the ‘gyroid’, which is found in many places:
• The physics of butterfly wings.
It turns out that the pattern of a gyroid is closely connected to the triamond:
• Matthias Weber, The gyroids: algorithmic geometry III, The Inner Frame, 23 October 2015.
Instead of trying to explain it here, I’ll refer you to the wonderful pictures at Weber’s blog.
http://phys.org/news/2016-06-x-ray-snapshot-butterfly-wings-reveals.html
New article about butterfly wing colors
Interestingly, it says butterfly wings may take advantage of topological defects. The paper is freely available here:
• Andrej Singer et al, Domain morphology, boundaries, and topological defects in biophotonic gyroid nanostructures of butterfly wing scales, Science Advances 2 (10 June 2016), e1600149.
Unfortunately it’s a bit short on clear explanations of what they found.
The light reflection off various paint may also contribute to the problem. Light and frequency reflection is a complex subject. Some of the pigments we paint with are somewhat iridescent; like a butterfly wing. This is a quantum effect that changes the frequency slightly depending on the direction it is viewed from. It’s not something we usually want but there are iridescent paints out there so be aware of them and experiment.
Complex! But make it simpler. Get the image up on your monitor, tweak it in whatever way you can until you like it. Now paint from it. I still use a printed image but I compare it to my monitor and paint accordingly. When I take a picture of the painting I adjust it until it looks like the painting. I still can’t guarantee that what you see on your monitor will match the painting exactly but no matter what I do I can’t guarantee that.
Thermoregulate with grace: butterfly wing scale structure
“As we as architects begin to think about designing not an object, but a process inspired by nature to generate objects, in short we will have no constraints. With the processes in our hands that allow us to create structures that we couldn’t even have dreamt of. And at one point we will build them.” — Michael Hansmeyer, TEDGlobal 2012
Physics of Butterfly Wings” [Azimuth]. Gorgeous images.